Nassim Haramein Egységes fizika Nassim Haramein több mint 30 évet töltött a fizika, a matematika, a geometria, a kozmológia, a kvantummechanika, a biológia, a kémia, valamint az antropológia és az ősi civilizációk összefüggéseinek kutatásával és felfedezésével. https://www.facebook.com/Nassim.Haramein.official/ Értsük meg a Fibonacci-sorozatot és az aranymetszést A Fibonacci-sorozat talán a természetben előforduló legegyszerűbb ismétlődő összefüggés. Ez a 0,1,1,2,3,5,8,13,21,34,55,89,144... számsorozat, amelyben mindegyik szám egyenlő a két előtte lévő szám összegével, illetve a két őt követő szám különbségével. Ez egy végtelen sorozat, amely növekedése során a végtelenbe tart.
Fibonacci számok http://www.akasha.de/~aton/AOHM1.htm Leonardo munkássága fellendülést jelentett a középkori európai matematikában. Az ókori görögök ugyan magas szintre fejleszették a matematikát, tudásuk nagy része azonban feledésbe merült, és ezt több mint ezer évvel később újra fel kellett fedezni. Ez az ókori rómaiak rovására írható, mivel őket csak a tételek gyakorlati felhasználása érdekelte. Leonardo Pisában született 1170 körül. Fiatal éveit atyja kívánságára Bougie-ban töltötte el, hogy jártasságot szerezzen az aritmetikai eljárásokban. Leonardo képzése messze túlment azon a határon, amire egy kereskedőnek vagy hivatalnoknak szüksége volt. Ezután tovább szélesítette matematikai ismereteit az Egyiptomban, Szíriában, Bizáncban, Szicíliában és Provenceban tett kereskedelmi jellegű utazásai során. 1240 után halt meg. 1202-ben írta a Az abakusz könyve (Liber abaci) című művét, amit jelentősen átdolgozott 1228-ban. Ez a figyelemre méltó könyv egyike volt azon fontos munkáknak, amelyek révén Európában elterjedt az új aritmetika és egyéb matematikai ismeretek. Leonardo hatalmas, az arabok munkáiból merített ismeretanyagot rendszerezett benne, egyes vonatkozásokban kiegészítette azt, mint ő maga mondta, Eukleidész geometriai művészetéből – lényegében tehát ugyanazon antik örökségből -, és mindehhez hozzátette még saját feladatait és módszereit. Az eredmény egy olyan munka lett, amelynek már a terjedelme is csodálatra méltó: Az abakusz könyve összesen 15 fejezetből áll és nyomtatott kiadásban 450 oldalt számlált, s hathatósan közreműködött a hindu – arab számrendszernek Nyugat – Európában való elterjesztésében. Fibonacci sorozat Leonardo Pisano, azaz Fibonacci nevét főleg a róla elnevezett rekurzív sorozat őrizte meg. Ez a következő feladatból született: Hány pár nyúl származik egy évben egyetlen pártól, ha minden pár havonta egy új párt szül, és minden új pár kéthónapos korától válik ivaréretté, és közben egyetlen nyúl sem pusztul el. A választ az 1+1+2+3+5+8+13+21+34+55+89+144=376 összeg adja, amelynek minden tagja – az első kettő kivételével – egyenlő az előző kettő tag összegével. Az összeadandókból alkotott számsorozatot Fibonacci sorozatnak nevezzük, és egy speciális esete a rekurzív sorozatok egy fontos osztályának. Erre a sorozatra az jellemző, hogy az elemeit néhány megelőző elem lineáris kombinációjával adhatjuk meg. A rekurzív sorozat elnevezés A. Moivre-tól származik (1724-ben tette közzé). Sok más módon is eljuthatunk a Fibonacci sorozathoz. Vázolunk néhány ilyen eljárást. I. A Százholdas Pagonyban a méhecskék fája úgy növekszik, hogy törzséből az első év végén kihajt egy ág. A fatörzs egy évet pihen, és csak a következő év végén hajt új ágat; az ág úgy viselkedik mint a fatörzs, tehát az első év végén hajt egy ágat, majd egy évet pihen, azután hajt újra. Az ágak sorra úgy hajtanak mint a törzs. Hány ága lesz a méhecskék fájának, ha 3,4,5,... évvel ezelőtt ültették? Itt az ágak számai alkotják a sorozatot. A leírásból világos, hogy ha valamely évben ismerjük az ágak számát, akkor a következő évben annyival több ág lesz, ahány az előző évben volt. II. Azt kérdezzük, hogy ha lépcső van előttünk és úgy akarunk felmenni az n-edik lépcsőre, hogy egszerre vagy egy, vagy két lépcsőt lépünk, akkor ezt hány különböző módon tehetjük meg. Az első lépcsőre egy módon léphetünk. A másodikra már két lehetőségünk van: kétszer egy – egy lépcsőt vagy egyszer két lépcsőt lépünk. A harmadik lépcsőre három különböző módon tudunk feljutni: háromszor egyet lépünk, egyszer egyet, egyszer kettőt lépünk, de akkor a sorrend is számít, tehát ez két különböző eset. Így a harmadik lépcsőre három különböző módon juthatunk fel. A negyedik lépcsőre való feljutások számát az előzőkhöz hasonlóan összeszámolhatnánk, de megpróbálhatjuk a feladatot az előző lépcsőkre való feljutások számának ismeretére visszavezetni. A negyedik lépcsőre úgy jutunk, hogy vagy a harmadikról egyet, vagy a másodikról kettőt lépünk. Ezért a negyedik lépcsőre annyi különböző módon jutunk fel, amennyi a második, illetve a harmadik lépcsőre való különböző feljutások összege 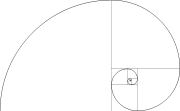
 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811 ... .http://www.hotdog.hu/titkokesrejtelyek/szimbolumok-titkosirasok Fibonacci számok Wikipedia Golden Ratio (Aranymetszés)Wikipedia |


 Az aranymetszés tetszőleges számú geometrikus formára alkalmazható, beleértve a köröket, háromszögeket, piramisokat, prizmákat és a sokszöget is. Az aranymetszés elve önmagában is képviseli a számok transzcendens voltát, és azt, hogy világunk megértése nem számokból áll, hanem abból, amit a számok képviselnek. A spirál segítségével az aranymetszés elve bemutatja, hogyan válnak a számok mennyiségből minőséggé. Végső soron minden minőség megjeleníthető a mennyiségekből. Mind a minőségi, mind a mennyiségi tulajdonságok csupán felcímkézett információk, összegyűjtött vitathatatlan tényeink.
Az aranymetszés tetszőleges számú geometrikus formára alkalmazható, beleértve a köröket, háromszögeket, piramisokat, prizmákat és a sokszöget is. Az aranymetszés elve önmagában is képviseli a számok transzcendens voltát, és azt, hogy világunk megértése nem számokból áll, hanem abból, amit a számok képviselnek. A spirál segítségével az aranymetszés elve bemutatja, hogyan válnak a számok mennyiségből minőséggé. Végső soron minden minőség megjeleníthető a mennyiségekből. Mind a minőségi, mind a mennyiségi tulajdonságok csupán felcímkézett információk, összegyűjtött vitathatatlan tényeink.