Aranymetszés, 2 - es (az elektronika alapvetően a kettes számrendszerre épül), 10 - es (az elektronikus műszerek általában tízes számrendszerben mérnek), 16 - os (memóriacímzésre a tizenhatos számrendszert használják) számrendszer.
Az emberek matematikájának ez az alapja évezredek óta.
Nem is lenne ebben semmi különös, hacsak nem ez jelenne meg az emberi test anatómiájában is.
Aranymetszés szabályai fedezhetőek fel a teljes testen, és az arcon is.
Minden embernek 2 szeme, 2 orrlyuka, 2 füle, 2 keze, 2 lába, 2 tüdője, 2 veséje, 2 örökítő szerve (herék, petefészkek) van.
Mindenkinek 10 kézujja és 10 lábujja található a testének végtagjain.
Ha sokáig elemezzük az emberi testet rá kell ébrednünk arra, hogy aki (akik) az első embereket létrehozta (létrehozták), az (azok) profi matematikus (matematikusok) volt (voltak).
Forrás: facebook
Szakrális geometria-- Aranymetszés--Spirális tudat
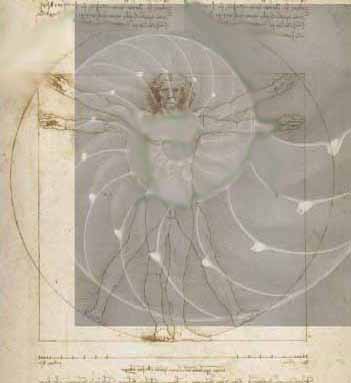 „Ahogy a számok szentek voltak a püthagoreusok számára, ugyanígy az ókori görögök a geometriát tekintették szakrális tudománynak- ez volt ugyanis az érvelés legmegfoghatóbb és ugyanakkor legelvontabb formája.”
„Ahogy a számok szentek voltak a püthagoreusok számára, ugyanígy az ókori görögök a geometriát tekintették szakrális tudománynak- ez volt ugyanis az érvelés legmegfoghatóbb és ugyanakkor legelvontabb formája.”
A geometriával számos dolgot le tudunk írni, meg tudunk magyarázni. A megfelelő számok és arányok gondos betartásával készült el nagyon sok ókori nép temploma, és egyéb szakrális helye. A geometria irányította az égi planéták mozgását és az évszakok változását.
A megalit építmények brit építészei és az egyiptomi piramisok tervezői egyaránt a szakrális geometriát alkalmazták építményeik helyének meghatározásában és tájolásában.
Min is alapszik a geometria? Az Euklidész által leírt geometriai alakzatokon: kör, háromszög, négyzet, valamint különböző arányokon, összhangokon.
(Az összhangon itt azt értem, hogy ismétlődésükben is van szabály)
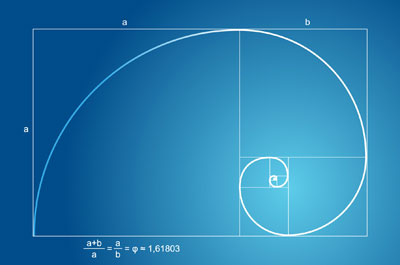 A felsorolt síkidomok, magukban is tiszta formák.
A felsorolt síkidomok, magukban is tiszta formák.
A szakrális arányokat bizonyos számokkal írták le, pl. ilyen a phi.
Szakrális:
Latin eredetű szó, jelentései:
- isteni, természetfölötti erővel, joggal, eredettel rendelkezőnek tartott
- szent, szentséges (dolog, személy), az istentisztelethez tartozó, vele kapcsolatos
- orvosi értelemben keresztcsonti
Így együttesen a szakrális geometria egy út, ami a geometriai formákon, arányokon keresztül egy olyan látásmódot és gyakorlatot ad, ami elősegíti a megtapasztalások sorozatát.
A szakrális geometria olyan geometria, mely szentsége annak nyilvánul meg, aki megfigyelő , aki felfedező.
A szó jelentését néha úgy is magyarázzák, hogy a szakrális geometria Isten nyelve, azoknak az embereknek az Istenéé, akik felfedezték és használni kezdték.
A szakrális geometriát jellemezhetjük mint vallásos vagy kultúrális értéket, melyet a matematikai összefüggések rajzos ábrái és a matematikai összefüggéseket szimbolizáló, ember alkotta tárgyak nyújtanak.
Az Aranymetszés arányszámát (golden ratio, ismertebb nevén Phi érték) gyakran használták a görög és római építészek építészeti terveikhez. Ennek a kifejezésnek jelenkori értelmezése egy feltételezett újra felfedezett matematikai szabályt ad az Univerzum valós természetére vonatkozóan, ez a szabály megnyilvánul a gabonakörökben vagy olyan ősi építészeti formákban is, mint pl. a Nagy Piramis vagy Stonhenge.
phi érték:


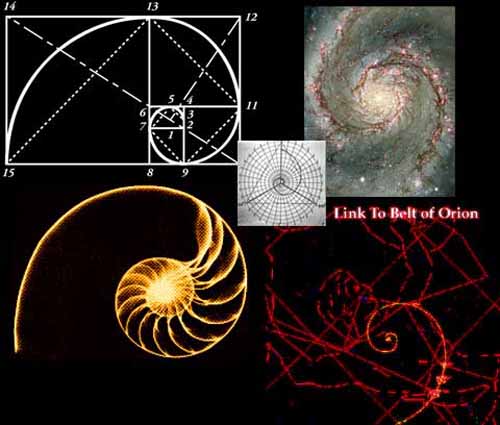
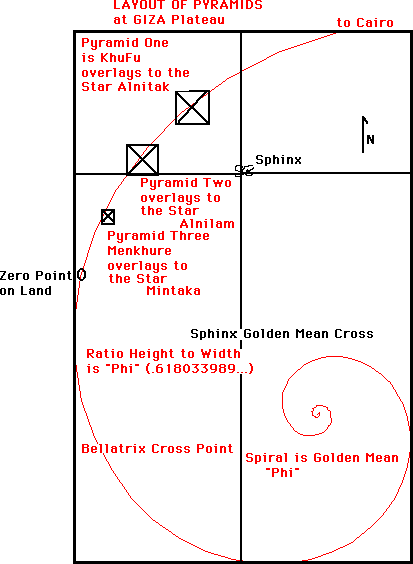 A Nagy Piramis geometriája
A Nagy Piramis geometriája
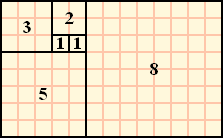
Négyzetek és rácsok
Az Aranymetszés, másik ismert nevén az isteni arány, vagy sectio divina irracionális szám, mely értéke
kb. 1.618 033 988 749 894 848. Ennek a számnak sok érdekes vonása van. Olyan formák hozhatóak létre
Aranymetszéssel, melyek régóta megfelelnek a nyugati kultúrák esztétikai ízlésének. Az Aranymetszést még ma is
gyakran alkalmazzák a művészek, építészek ha természetes egyensúlyt akarnak kifejezni a szimmetria és asszimmetria
között.
Pithagorasz követői, akik a számokat arányokban határozták meg (nem egységekben) abban hittek, hogy a valóság
számtani és az Aranymetszés a létezésről szóló alapigazság.
A DAVINCI-KÓD

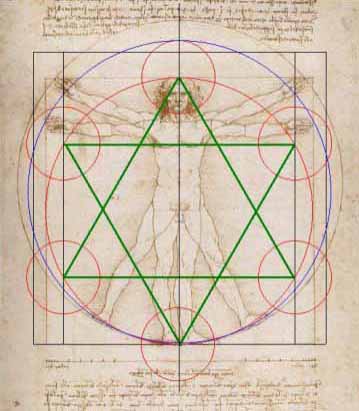
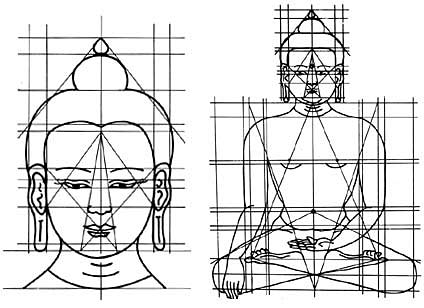
Aranymetszés--Spirális tudat Dávid-csillag A tudat mozgása

teremtés geometria - 12 az 1 körül
Az Univerzumot a gondolat teremtette, mely a fizikai valóságban manifesztálódik geometriai összefüggésekben, ezt
nevezzük szakrális geometriának. A szakrális geometria ciklusokban ismétlődik így egy lineáris idő illúzióját adja, minek
segítségével megtapasztalhatjuk az érzelmeket. A "szakrális geometria" kifejezést használják régészek, antropológusok,
és matematikusok arra, hogy meg tudják magyarázni mindazokat vallási, filozófiai és spirituális gondolatokat, melyek a
geometria körül felbukkantak a történelem során a különböző kultúrákban. Ez egy mindent-átfogó kifejezés, mely magában
foglalja a pitagoraszi geometriát, a neo-plátoni geometriát, úgy mint az organikus és logaritmikus görbék között érzékelt
összefüggéseket. "
Kiegészítés : Aranymetszés

,,
Az aranymetszés vagy aranyarány egy olyan arányosság, ami a természetben és művészetben is
gyakran megjelenik, természetes egyensúlyt teremtve a szimmetria és az aszimmetria között.
Aranymetszési arányok találhatók számos ókori épületen, középkori és reneszánsz
képzőművészeti alkotásokon. Az ókori pitagoreusok (Pithagorasz és követői), akik szerint a
valóság matematikai alapokon nyugszik, az aranymetszésben a létezés egyik alaptörvényét
vélték felfedezni, ugyanis ez az arány felismerhető a természetben is (például az emberi testen
vagy csigák mészvázán).
Az aranymetszés arányait tartalmazó formák máig nagy esztétikai értékkel bírnak, számos
területen (például atipográfiában vagy a fényképészetben) alkalmazzák őket.
Az aranyarányt numerikusan kifejező irracionálisΦ ≈ 1,618 számnak (görög nagy fí) számos
érdekes matematikai tulajdonsága van.
Gyakori megjelenése miatt a geometriában már ókorimatematikusok is tanulmányozták az aranymetszést.
Bizonyíthatóan az ókori Egyiptomban is értették és használták ezt a törvényszerűséget. Az i. e. 2600 körül épült
gízai Nagy-piramis arányaiban is felfedezhető az aranymetszés aránya. A piramis alapélének a fele (átlag 186,42 m) és
oldallapjainak a magassága (kb. 115,18 m) az aranymetszés szerint aránylik egymáshoz (0,03%-os eltéréssel, ami
hibahatáron belülinek tekinthető).
Az ókori görögök is ismerték ezt az arányt. Pithagorasz,Theodorus és Euklidész
is foglalkozott vele. Az aranymetszés jelölése, a Φ (görög nagy fí betű) Pheidiász
görög szobrász nevéből származik, aki gyakran alkalmazta munkájában.
(1810–1876) Aus experimenteller Ästhetik (A kísérleti esztétikából) című művében ír nagyszámú emberen végzett
méréseiről. A jól kifejlett emberi alaknak első osztási pontját a köldökre tette és megállapította, hogy a test törzsének és
főbb tagjainak illeszkedési pontjai szintén az aranymetszés szerint aránylanak. Kétségtelen, hogy a korábbi, különösen a
görögszoborművek arányai is megfelelnek Zeising elméletének: ha a test magassága 1000, a test alsó része a köldöktől
618, a test felső része a köldöktől 382, a fej hossza pedig 146. Ezek mind az aranymetszési szabály szerint viszonyulnak
egymáshoz. Zeising azonkívül megkísérelte az ókor és a középkor legkiválóbb építményein
kimutatni, hogy azoknak egészén és egyes részeinek méreteiben az aranymetszés elve uralkodik, ahogy a festészet
legismertebb alkotásainak elrendezésében is ugyanez az elv érvényesül.
Az ókorban isteni számnak is nevezték, ugyanis az emberek nem csak matematikai tényként tekintettek rá, hanem az
istenség földi jelenlétének és a teremtésnek a kifejezőjeként is értelmezték."
Aranymetszés avagy phi a testen
Aranymetszés, mint speciális arányt, szokták úgy is emlegetni, hogy "divina proportione", azaz az "isteni arány".
Definíció
Aranymetszésrõl beszélünk, amikor egy mennyiséget, illetve egy adott szakaszt úgy osztunk két részre, hogy a kisebbik
rész úgy aránylik a nagyobbikhoz, mint a nagyobbik rész az egészhez.
a = p + q Aránypárral:
p : q = q : (p + q)
Zeising német esztéta az 1800-as évek közepén az aranymetszésben vélte megtalálni az emberi test szépségének az okát, sõt
a természeti tárgyak, élõlények és mûvészeti alkotások uralkodó morfológiai elvét. (morfológia: alaktan) Zeising
természetesen túlzott.
Phi az arcon.
 Leonardo megmérte az ember csontszerkezetének pontos arányait. Õ volt az elsõ, aki kimutatta, hogy az emberi test a szó szoros értelmében építõkövekbõl áll, amelyek arányszáma mindig a phi-vel egyenlõ. Mi valójában valamennyien két lábon járó emlékmûvei vagyunk az aranymetszésnek.
Leonardo megmérte az ember csontszerkezetének pontos arányait. Õ volt az elsõ, aki kimutatta, hogy az emberi test a szó szoros értelmében építõkövekbõl áll, amelyek arányszáma mindig a phi-vel egyenlõ. Mi valójában valamennyien két lábon járó emlékmûvei vagyunk az aranymetszésnek.









Az aranymetszés az ember tökélyre törekvésének legmagasabb stádiuma. Olyan szabály, amit a matematika, az építészet, a mûvészet és a természettudományok egyaránt felfedeztek és használtak. Mágikus eredete ismeretlen, csupán az alkalmazásából tudhatjuk, hogy már évezredek óta jelen van az emberi alkotásokban.
Alapja a phi (fi) számban rejlik. A phi-t a legszebb számnak tekintik a világegyetemben. A phi szám a Fibonacci-sorozatból vezethetõ le. Ez a haladvány arról híres, hogy az egymást követõ számok összege megegyezik az utánuk jövõvel, és arról is, hogy az egymás melletti számok hányadosának az az elképesztõ sajátossága, hogy mindig 1,618-at tesz ki (1996-ban tízmillió számjegyig adták meg az értékét, és a számjegyek sorozatai soha nem ismétlõdtek).
A phi szám látszólag misztikus matematikai eredete dacára, a phi legészbontóbb tulajdonsága mégis az, hogy a legelemibb építõkõ szerepét játssza a természetben. A növények, az állatok, de még az emberi lények térbeli sajátosságai is kísérteties pontossággal mutatják a phi az 1-hez arányt.
A phi mindenütt jelen van a természetben, ami nem lehet véletlen, ezért tekintették az ókoriak a phi-t a világegyetem teremtõje által megszabott számnak.
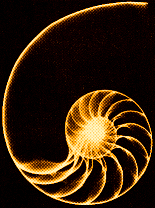
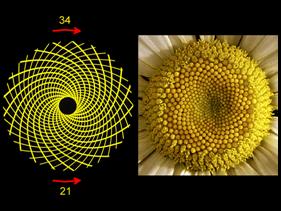
Az elsõ tudósok isteni arányszámnak vagy aranymetszésnek nevezték. A legismertebb példák: a nautilusz-kagylóhéj egyik spiráljának átmérõje a másikhoz a phi-t adja. A méhkaptárban a nõnemû egyedek száma a hímnemû méhekéhez szintén phi. A napraforgómagok ellentétes csigavonalakban helyezkednek el. A két szomszédos sor átmérõje közti arányszám a phi. A fenyõtobozok, a levélelrendezésû növényi szárak, a rovartest részei mind-mind az aranymetszés szabályának engedelmeskednek.
A phi rendkívül fontos szám a mûvészetben. Leonardo da Vinci híres férfialakja, a Vitruvius-tanulmány, amely Marcus Vitruviusról, a nagyszerû római építészrõl kapta a nevét, aki a "De Architectura" címû munkájában dicsõítette az aranymetszést.
Leonardo megmérte az ember csontszerkezetének pontos arányait. Õ volt az elsõ, aki kimutatta, hogy az emberi test a szó szoros értelmében építõkövekbõl áll, amelyek arányszáma mindig a phi-vel egyenlõ. Mi valójában valamennyien két lábon járó emlékmûvei vagyunk az aranymetszésnek.
A káosz mögött rend uralkodik a világban. Amikor az ókoriak felfedezték a phi-t, meg voltak gyõzõdve, hogy Isten építõkövére akadtak, és leborultak a természet nagysága elõtt.
Az ember csupán játszadozik a természet törvényeivel, és mivel a mûvészet az ember arra tett kísérlete, hogy utánozza a Teremtõ mûvének szépségét, az aranymetszés sok példájával találkozunk a mûvészetben. Michelangelo, Albrecht Dürer, Leonardo da Vinci - szigorúan ragaszkodtak az aranymetszéshez a kompozícióik elrendezésében.
Az építészetben: az athéni Parthenón, az egyiptomi piramisok, az ENSZ székháza New Yorkban.
Az aranymetszés szervezõ struktúra Mozart szonátáiban, Beethoven V. szimfóniájában; Bartók, Debussy és Schubert zenemûveiben.
Az aranymetszéssel kapcsolatban mindig megjelenik egy szimbólum: a pentagramma vagy ötszög - ahogy a régiek tisztelték - isteni és mágikus jelkép. Ha felrajzolunk egy ötszöget, oldalai automatikusan az aranymetszés szabályai szerint osztódnak részekre, a vonalszakaszok arányai az ötszögben mindig phi-vel egyenlõk. Ezért vált ez a szimbólum az aranymetszés jelképévé, és ezért a szépség és tökéletesség jelképe, amely az istennõre, a szent nõiességre utal.
Feldolgozta Cziría Attila (Atelier, 2005/4)
(Fibonacci 1170-ben született az itáliai Pisában. Az észak-afrikai Bugiában - a mai Bendzsájában - nõtt fel, itt folytatott tanulmányokat, majd 1200 körül visszatért Pisába. Fibonacci munkásságában határozottan felismerhetõ az arab matematikusok hatása, akik talán tanították is ott töltött évei során. Fibonacci számos matematikai értekezést írt, és jelentõs matematikai felfedezéseket tett, amelyek nagyon népszerûvé avatták õt Itáliában. 1250-ben halt meg.)
Az aranymetszés szerint egy kompozíció két része akkor aránylik tökéletesen egymáshoz, ha a kisebb rész úgy aránylik a nagyobbhoz, ahogyan a nagyobbik aránylik az egészhez...
Kapcsolódó irodalom:
http://www.scribd.com/doc/19711451/Tiltott-Termeszeti-torvenyek
Az aranymetszés története
Nem hiszem, hogy az isteni harmónia kifejezhető volna egy számmal, azt azonban annál valószínűbbnek tartom, hogy ennek a harmóniának létezik egy algebrailag is kifejezhető vetülete. Talán nem is a vagyontárgyaink összeszámlálására találták fel az algebrát? Lehetséges, hogy az algebra olyan filozófiai tételeket tartalmaz, amik például a harmóniát is meghatározzák?
 Adjunk egy kis szabadságot az elménknek! A harmónia a dolgok, események, érzelmek egymáshoz fűződő viszonya, amit mindig egy esztétikai értékrend és a mögötte álló filozófia határoz meg. Létezik-e az abszolút harmónia? Mert ha igen, akkor a korreláció fordított, s nem az értékrend és filozófia határozza meg az abszolút harmóniát, hanem inkább emez definiálja amazokat. Márpedig az abszolút fogalmak kifejezhetők, vagy mondjuk úgy, tömöríthetők az algebra nyelvén.
Adjunk egy kis szabadságot az elménknek! A harmónia a dolgok, események, érzelmek egymáshoz fűződő viszonya, amit mindig egy esztétikai értékrend és a mögötte álló filozófia határoz meg. Létezik-e az abszolút harmónia? Mert ha igen, akkor a korreláció fordított, s nem az értékrend és filozófia határozza meg az abszolút harmóniát, hanem inkább emez definiálja amazokat. Márpedig az abszolút fogalmak kifejezhetők, vagy mondjuk úgy, tömöríthetők az algebra nyelvén.
Az aranymetszés a tárgyaknak egymáshoz fűződő arányáról beszél, a mozdulatok, valamint a térből kimetszett terek és idomok kapcsolatáról szól. Rögtön fölmerül egy fontos kérdés: mit mivel arányítsunk? Milyen párokat vagy viszonyrendszereket állítsunk fel? Egy közönséges szék esetében vizsgálhatjuk a háttámla és a lábak arányát, vagy az ülőfelület és a háttámla arányát. Ez a viszonyszám lehet területi arány, de az sem biztos, hogy idomokat kell arányítanunk, lehet térfogatot térfogattal. Az első lépés tehát az aránypárba állítandó alapegységek beazonosítása.
 Mindig is vonzott a tánc művészete, leginkább az indiai klasszikus táncok ragadtak meg. A nyugati festőművészetben talán Degas táncosnő-képei a legismertebbek. Ezek a balerinák szinte súlytalanok, tökéletes arányokkal mozdulnak, a képeken a tánc éteri minősége tölti fel testüket és ruházatukat. Szerettem volna tetten érni a légiesség eme technikai lényegét. Magam is próbálkoztam a táncoló női alak ábrázolásával, kucsipudi, manipuri és kathaki táncosnőket rajzoltam meg. Az első pillanatban azt gondolná az ember, egy-két könnyed vonal, és kész is az alkotás. A valóság azonban kicsit eltér ettől. A tánc – és főként az indiai klasszikus tánc – mozdulatai mértani pontosságúak, valószínűleg nem tudatosan, inkább rutinszerűen. A kép csak akkor sikerülhet, ha megtaláljuk az arányokat, és szinte megszerkesztjük a képet mozdulataiban.
Mindig is vonzott a tánc művészete, leginkább az indiai klasszikus táncok ragadtak meg. A nyugati festőművészetben talán Degas táncosnő-képei a legismertebbek. Ezek a balerinák szinte súlytalanok, tökéletes arányokkal mozdulnak, a képeken a tánc éteri minősége tölti fel testüket és ruházatukat. Szerettem volna tetten érni a légiesség eme technikai lényegét. Magam is próbálkoztam a táncoló női alak ábrázolásával, kucsipudi, manipuri és kathaki táncosnőket rajzoltam meg. Az első pillanatban azt gondolná az ember, egy-két könnyed vonal, és kész is az alkotás. A valóság azonban kicsit eltér ettől. A tánc – és főként az indiai klasszikus tánc – mozdulatai mértani pontosságúak, valószínűleg nem tudatosan, inkább rutinszerűen. A kép csak akkor sikerülhet, ha megtaláljuk az arányokat, és szinte megszerkesztjük a képet mozdulataiban.
Az aranymetszés matematikája
Sokan sokat foglalkoztak már az aranymetszés témájával, könyvtárnyi irodalom áll rendelkezésre. Hadd tekintsük át röviden az aranymetszés jelentését és történelmi hátterét! Maga a tétel nem túl bonyolult: aranymetszésről akkor beszélhetünk, ha például egy két részre osztott szakasz két része úgy aránylik egymáshoz, mint ahogy a nagyobbik rész aránylik a teljes szakaszhoz. Vagyis a nagyobbik rész az egész és a kisebbik rész mértani középarányosa.
A fentiekkel egyenértékű az a megfogalmazás, miszerint a nagyobbik rész úgy aránylik a kisebbik részhez, mint a kisebbik rész a két rész különbségéhez:
Itt érhető tetten az aranymetszés titka: a fent említett esetekben mindig egy állandó arányszámot kapunk. Az arányszám jelölésére a görög phi betűt használjuk, melynek értéke 1,618…. A jelölés Phidiasz görög szobrász nevéből származik. Pontosabb értéke:
A phi -vel először írásos formában Eukleidész Elemek című művében találkozunk. A II. könyv 11. tétele a következőképpen hangzik: „Adott egyenest osszunk fel úgy, hogy az egészből és a részek egyikéből alkotott téglalap egyenlő legyen a másik rész négyzetével.” (Gajdácsi Glória szakdolgozata alapján)
Az aranymetszéssel már az ókorban is foglalkoztak, Egyiptomban valószínűleg ismerték a phi-t. A gizai piramis szerkesztésében is érvényesül az aranymetszés, mert az alapél fele és az oldallap magassága ezt az arányt mutatja.
Mint a fentiekben láttuk, az aranymetszés a görögök számára sem volt ismeretlen, s az indiaiak is foglalkoztak vele. Hémacsandra (1089-1172) dzsainista író a szanszkrt költészet ritmusát vizsgálta. A szótag a szanszkrtban lehet hosszú és rövid. A hosszú szótag kétszer olyan hosszú, mint a rövid. Hémacsandra azt a kérdést tette fel, hány formája lehet a ritmus motívumainak. Sokat foglalkozott a nyelvtan, filozófia, tradíció és a korabeli történelem kapcsolatával, s a verselésben ismerte fel a misztikus arányt. Kutatásai során az Európában Fibonacci-számként ismert sorozathoz jutott el 1150-ben, jó 50 évvel korábban, mit az olasz tudós. Hémacsandra Gudzsarát államban, Dhandhukában született, Ahmadabadtól 50 kilométerre délnyugatra. Szüleitől a Csandradéva nevet kapta. Fiatalon szerzetesnövendékként élt egy dzsainista templomban és felvette a Szómacsandra nevet. 1110-ben a svétambara rend tagja lett, s az Ácsárja Hémacsandra nevet kapta. Tudományos mestere Gopála, a matematikus volt.
Hémacsandra Kumárapála uralkodó (1143-73) tanácsadójaként működött. Összeállította a szanszkrt és prákrt nyelv grammatikáját, s írt az indiai filozófia minden irányzatáról. Legismertebb műve A hatvanhárom nagy ember élete.
Miért küszködtek a világ különböző részein ezzel a bonyolult arányszámmal, s pontos mértani megszerkesztésével? Mit sejtettek meg az egyiptomi, görög és indus tudósok? A matematikát a tudományok tudományának nevezik, amely állítás az aranymetszés kapcsán is beigazolódni látszik. A költészetet, a szobrászatot, a festészetet és a zenét, s mint később láthatjuk, a tudomány egészét az algebra és geometria fűzi egybe, hiszen a matematika mindegyikben jelen van. Ráadásul a matematika nem egyszerűen jelen van, hanem a különböző szakterületeken azonos összefüggéseket tesz láthatóvá, mintha egy másik, közös síkon jelenítené meg a valóságot. Talán a matematika adja kezünkbe az ismeretlen teremtés kulcsát? Vizsgáljuk meg az aranymetszés geometriáját! (1. ábra)
A szakasz megszerkesztése és a szabály szerinti felosztása nem evidens, az ötszög szerkesztéséhez viszont mindenképpen ismerni kellett. A 72 fokos szögek geometriája már ismert volt Eukleidész vagy Pitagorasz számára. Első lépésként egy speciális egyenlő szárú háromszöget szerkesztettek, olyat, melynek az alapon álló szögei kétszer akkorák, mint a csúcsszög. Így alakult ki az aranyháromszög (72, 72, 36 fokos szögek). (2-4. ábra)
A szerkesztésnek több útja is lehetséges, de minden esetben szükségünk van az arany háromszögre, valamint a phi ismeretére és használatára. (5-6. ábra)
Ilyen módon vált lehetségessé a pentagram és az ötágú csillag pontos megszerkesztése is, aminek az okkultizmusban jelentős szerepe volt. Nem állíthatjuk, hogy a pentagram negatív szimbólum volna, hiszen az isteni arányszám az alapja. Szinte minden okkult könyvben találkozhatunk vele, innen eredhet negatív felhangja. Az okkult tudományok ismerői a teremtés aktusát akarták megragadni vele.
Az öt gyakran jelenik meg a mitológiában is. Az indiai tradícióban az öt elem – föld, víz, tűz, levegő, éter – alkotja az akasa-univerzumot. Kínában kicsit másként fogalmazzák meg az elemeket, csakúgy, mint a druidáknál: víz (tenger), föld (fém), tűz (szél), levegő (ég), természet (fa), de lényegileg ugyanarról van szó. A pentagram tulajdonképpen nem más, mint két egymásra csúsztatott háromszög, vagy öt aranyháromszög egy középpont köré rendezve. Az ötágú csillag egy álló alak rajzként a mikrokozmosz és az ember jelképe, így ember-jegy, az embert magát jelzi, egyben a cselekvés jelképe is. Érdekes párhuzam az ember öt-öt ujja. Püthagorasz követői a tízes mellett az ötöst is tökéletes számnak tartották, Babilonban pedig az egészséggel feleltették meg.
Az aranymetszés témájával foglalkozva, mindenképpen meg kell említenünk Fibonaccit, azaz Leonardo Pisanot, a XII-XIII. század fordulóján alkotó olasz matematikust, aki a tízes alapú helyi értékes számrendszer egyik meghonosítója volt. Mint ismeretes, a helyi érték rendszer arab közvetítéssel jutott el Európába. A Liber Abaci című munkájában egy olyan számsorozatról beszél, ami nagyon megközelíti a phi értékét, ahogy ezt az ábrán is láthatjuk.
Fibonacci 1170-ben született az itáliai Pisában. Az észak-afrikai Bugiában – a mai Bendzsájában – nőtt fel, itt folytatott tanulmányokat, majd 1200 körül viszszatért Pisába. Fibonacci munkásságában határozottan felismerhető az arab matematikusok hatása, akik talán tanították is ott töltött évei során. Fibonacci számos matematikai értekezést írt, és jelentős matematikai felfedezéseket tett, amelyek nagyon népszerűvé tették őt szerte Itáliában. 1250-ben halt meg. (7. ábra)
A Fibonacci-számsorban a sorozat harmadik elemétől kezdve bármely tag az azt megelőző két tag összege:
Az aranymetszésre visszagondolva, tekintsük a teljes szakaszt 1000-nek. Ekkor az aranymetszés szabályai szerint az arány a következőképpen alakul:
Kerekített értékek: 2, 3, 5, 8, 13, 22, 36, 58, 90, 146, 236, 382, 618, 1000, …….. A Fibonacci által kapott összefüggés formailag hasonló az aranymetszésnél kapott egyenlethez, és (a harmadik elemtől) alkalmas a sorozat előállítására:
és így tovább. Az első néhány Fibonacci-szám: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946…
A kapott arány akkor egyezne meg az aranymetszéssel, ha a Fibonacci-sorozat egymást követő elemeinek hányadosa ugyanaz az érték lenne, vagyis az elemek geometriai sorozatot is alkotnának. Az elemek számának növelésével azonban ez a hányados egy állandó számhoz, az aranymetszéssel kapott arányához közelít.
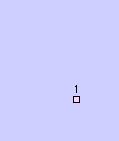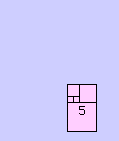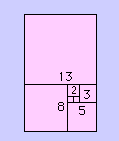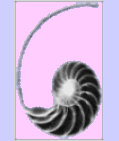
Négyzetek segítségével is ábrázolhatjuk a sorozatot (8. ábra), ahol F1 és F2 egy-egy egységnyi négyzet (1- 1). A föléjük helyezett F3 oldallapja két egységnyi lesz (2). A mellé helyezett F4 oldala F2 + F3 lesz, és így tovább. Az egymást követő négyzetek aránya azonos a Fibonacci-sorozat arányaival. Nézhetjük úgy is, hogy az első téglalap (F1 és F2 együtt) oldalainak aránya, illetve a második téglalap (F1, F2, F3) oldalainak hossza azonos lesz a Fibonacci-sorozat számaival.
Aranymetszés a tudományban
A kvázi-kristályok esetében fedezték fel az úgynevezett arany rombuszokat, melynek szögei 72 és 108 fokosak, ezek a Penrose-csempék. Roger Penrose a XX. század hetvenes-nyolcvanas éveiben foglalkozott a témával. A felfedezésnek nagy jelentősége volt a kristályok kutatásában. A rombuszok belső terei az aranymetszés arányait mutatják (9. ábra)
Penrose 1976 májusában a következőket írta kollégájának, Gardnernek: „Az is lehetséges, hogy e fölismerések a biológia szempontjából is jelentősek lehetnek. Ne feledjük, hogy bizonyos vírusok szabályos dodekaéder és ikozaéder alakban növekednek. Mindig is zavarba ejtő kérdés volt, hogyan csinálják ezt? Ammann nem-periodikus testeivel viszont, mint alapegységekkel, kváziperiodikus „kristályokhoz” juthatunk; olyan, kristálytanilag látszólag lehetetlen hasadási irányokkal, melyek síkjai dodekaédert vagy ikozaédert határoznak meg. Lehetséges, hogy a vírusok növekedése is ilyesfajta nem-periodikus egységen alapul – vagy túlságosan merész ez az elképzelés?”
A természetben számos helyen találkozhatunk olyan formációkkal, melyek az aranymetszés arányait viselik magukon: csigavonalban, a levelek elrendezésében, sejteken belül, vírusoknál vagy más területeken. Létezik az úgynevezett arany szög is, amely cos = 0,618034… A szög értéke: = 51°49’43”. Ezzel a szöggel találkozhatunk például Krisztus-monogram X-e és a P betű szárai között vagy Szent István betűjelénél (10. ábra).
Az aranytéglalap oldalainak aránya megegyezik a phi értékével (11. ábra)
Platonikus testeknek nevezzük a szabályos testeket, vagyis azokat a konvex poliédereket, melyeknek élei, élszögei és lapszögei egyenlők. Összesen öt ilyen test létezik: a tetraéder, a hexaéder, az oktaéder, a dodekaéder és az ikozaéder, melyek közül az utóbbi három vizsgálható az aranymetszés szempontjából. Az oktaéder egy ikozaédert rejt magában oly módon, hogyha az oktaéder éleinek aranymetsző pontjait összekötjük, egy ikozaédert kapunk eredményül (12-14. ábra)
Aranymetszés a művészetben
A reneszánsz korában többen behatóan tanulmányozták az emberi test arányait. Leonardo da Vinci a festészetről szóló művének (latin címe Trattato della Pittura) hetedik fejezetében tárgyalja az emberi test arányait és mozdulatait. Leonardo a csontok arányait mérte és kutatta. Ezt a tevékenységét, amit később az elhíresült rajzon mutatott be, Marcus Vitruvius magasztalta munkájában. Később Luca Paccioli könyvet írt az isteni arányról (latinul Divina Proporzione). Albrecht Dürer szintén írt a tárgyról, de ide tartozik Gottfried Schwadow könyve is az emberi test arányairól, 1834-ből.
Az aranymetszésről többnyire mindenkinek Leonardo Vitruvius-tanulmánya jut eszébe (lásd a nyitó képen), pedig az aranymetszéssel az élet, a természet számos területén találkozhatunk. Ezt a matematikai tételt mégis a művészet tette közismertté a harmónia, a szépség szimbólumaként. Az aranymetszést a festészet és a szobrászat számos területén alkalmazták. Dürer és Michelangelo is az aranymetszés szabályai szerint komponálta alkotásait, s itt kell említsük Csontvári Kosztka Tivadart, a Napút festőjét is. Képeinek táblája, belső szerkezete szigorúan tervezett volt, s az a komponáltság nyugalmat sugároz, a nézőben a teljesség érzetét kelti. A képekből nem hiányzik semmi, de elhagyni sem lehetne róluk semmit. Csontvári esetében a térbeli határok egybemosódó megfogalmazása sem töri meg ezt a harmóniát.
Az építészet és a szobrászat is felhasználta az aranymetszés ismeretét, már a piramisépítészettől kezdve. Az ókorban az emberi test arányait alkalmazták az építészetben is. Az arány szerepe a költészetben talán kevésbé ismert, pedig itt is nagy fontosságú. Egy zeneműnek – éppúgy, mint bármely más alkotásnak – az arányai adják meg a tetszetős méreteit. Bartók zenéjének szerkezetében a tobozok csavarodásának spirálja figyelhető meg. A színpadi művekben, a drámákban majdnem kiszámítható az egyes fölvonások és jelenetek közti arány. Elterjedt a hosszú expozíció a gyors és csattanós befejezés mellett. Az arány, mint szerkesztési elv a jellemeknek egymáshoz viszonyulásában, a párbeszédek méreteiben és sok egyéb strukturális egységben is mutatkozik. Az arányosság alkalmazásának ugyanakkor könnyednek és természetesnek kell lennie, mert ha az alkotáson átsüt a kiszámítottság, hűvös és élettelen lesz a mű.
Úgy tűnik, a matematika olyan lehetőségeket rejt magában, ami a titkos tudományok egyik alappillérévé tette, vagy talán fordítva, belőle virágzott ki az ezotéria sok-sok ága. A rendkívül szerteágazó vizsgálódásoknak se vége, se hossza. Lassan apró részeire bontottuk az anyagvilágot, de még mindig hiányzik valami, ami értelmezi a rendszert, és kapcsolatot teremt a feltárt valóság legtávolabbi részletei között is. Ilyen természetes algoritmus lehet az aranymetszés, az isteni arányosság alapja. Ez a jelenségekben benne rejlő kulcs, a magasabb minőség matematikai vetülete, ami az élet számos területén ott rejtőzik, hol szemmel láthatóan, hogy ismeretlenül. A művészi arányosság vizsgálata olyan pont, ahol az isteni harmónia számunkra is észlelhetővé válik.
Összeállította: Ubornyák Katalin
Matematikai szakértő: Erdélyi Ferenc
AZ ARANYMETSZÉS EZOTERIKUS TITKAI
Az alábbiakban összefoglaltam az aranymetszéssel kapcsolatos közismert dolgokat, valamint mindazon titkokat, amikről eddig csak nagyon kevés beavatott tudott. Az aranymetszés ismerete kulcsfontosságú a teremtés működésének megértéséhez egy bizonyos beavatási szint fölött, amikor a matematikai összefüggések vizsgálatával foglalkozik az ember. A közismert tényeket az internetről vadásztam össze, a többit a beavatásaim során az égi mesterektől tanultam. Biztos vagyok benne, hogy a következő évszázadokban még sok izgalmas titok fog feltárulni a témát kutató elmék előtt ebben a tárgykörben, ami segít kiterjeszteni és pontosítani az időfizikai és időmatematikai modelleket.
1. AMI KÖZISMERT
Euklidesz Elemek című művében szerepel a következő mondat: "Adott egyenest osszunk fel úgy, hogy az egészből és a részek egyikéből alkotott téglalap egyenlő legyen a másik rész négyzetével."
Egyszerűbben megfogalmazva a feladatot: Ha egy szakaszt egy pont úgy oszt két részre, hogy a kisebbik szakasz úgy aránylik a nagyobbikhoz, mint a nagyobbik az egészhez, akkor a pont a szakasz aranymetsző pontja. Egységnyi hosszúságú szakasz esetén az aranymetsző pont kb. 0,618... egységre van az egyik végponttól. Az aranymetszés arányszáma egy végtelen tizedes tört, ami a (1+sqrt5)/2 képlettel írható fel a legegyszerűbben. Ennek értéke közelítően: 1,618033988749894848204586...
Ezt a számot a görög fi betűvel szokták jelölni, ami egy Pheidiasz nevű ókori görög szobrász nevének első betűjéből származik. Ő használta a szobrainak elkészítéséhez az aranymetszést, amit többféleképpen lehet körzővel és vonalzóval szerkeszteni.
Egy Zeising nevű német esztéta az 1800-as évek közepén az aranymetszésben vélte megtalálni az emberi test szépségének okát, mivel a testünk részei általában ezt az arányt követik. Ilyen az ujjpercek hossza az ujjhoz képest, az ujjak hossza a tenyérhez képest, a kéz hossza az alkarhoz képest, stb. Az építészetben az olyan ablakokat, ajtókat, homlokzati elemeket, méretarányokat találjuk szépnek, amik oldalaránya fi. Emiatt például a nyomdászatban az aranymetszés olyan klasszikus arányrendszerré vált, amely meghatározza a főbb oldalelemek egymáshoz való viszonyát. Segít a szedéstükör, a margók, a címek és a betűméret megtervezésében.
A pentagon (szabályos ötszög) belső szögeinek nagysága 108°. Ennek körzővel és vonalzóval való megszerkesztésekor szintén használni kell az aranymetszést. Euklidesz úgy szerkesztett ötszöget, hogy először készített egy olyan háromszöget, aminek az alapjánál lévő szögei kétszer akkorák, mint a csúcsában lévő szög (36°, 72°, 72°). Ez az aranyháromszög, amely oldalainak aránya fi. Ezt a háromszöget kell beilleszteni egy adott sugarú körbe, hogy megkapjuk a szabályos ötszöget.
A szabályos ötszögből lehet készíteni a pentagrammát (ötágú csillagot), amikor 5 db aranyháromszöget körben ráteszünk az ötszögre. A pentagrammát hívják csodálatos ötszögnek, bűvös ötszögnek, misztikus ötszögnek, csillagötszögnek, boszorkányszögnek, Salamon pecsétjének, Pitagorasz csillagnak is. Ez ősidők óta az egység és az univerzum szimbóluma, de jelképe az egészségnek, termékenységnek és az életnek is. Jelképként használják a boszorkányok, okkultisták, püthagoreusok, szabadkőművesek, kommunisták, valamint számos ország zászlaján és címerében megtalálható, különféle színekben.
A pentagramma tehát öt darab aranyháromszög egy ötszög köré rendezve. Ha egy pentagrammát testhálóként értelmezünk, egy szabályos ötszög alapú gúlát láthatunk benne. Ha ilyen gúlákat illesztünk egy dodekaéder lapjaira, akkor egy csillag poliédert, pontosabban kis csillag dodekaédert kapunk.
Platonikus testeknek nevezzük a szabályos testeket. Ezek olyan konvex poliéderek, amik élei, élszögei és lapszögei egyenlők. Az élek és élszögek egyenlőségéből következik, hogy a szabályos test lapjai egybevágó szabályos sokszögek, lapjai tehát ugyanannyi oldalúak. Az élszögek és a lapszögek egyenlőségéből következik, hogy a szabályos testszögletei egybevágó szabályos szögletek, tehát ugyanannyi élűek. Három dimenzióban összesen öt ilyen test létezik. Ezek (lapszám szerinti sorrendben) a tetraéder, a hexaéder (kocka), az oktaéder, a dodekaéder és az ikozaéder. Ez utóbbi három vizsgálható az aranymetszés szempontjából is.
A legfeltűnőbb kapcsolat az ikozaéder és oktaéder között figyelhető meg, mivel az oktaéder egy ikozaédert rejt magában. Ha az oktaéder éleinek aranymetsző pontjait összekötjük, egy ikozaédert kapunk.
Az aranytéglalap oldalainak aránya fi. Ha három aranytéglalapot speciális helyzetbe állítunk, azaz egymásra merőleges és egymást metsző helyzetbe hozunk, a kapott "térkereszt" éppen egy ikozaédert eredményez. Ebből a vázból úgy juthatunk az oktaéder vázához, hogy a téglalapokat négyzetekké egészítjük ki. Az aranytéglalap és a köré írható négyzet úgy helyezkednek el egymáshoz képest, hogy a négyzet oldalainak megfelelő aranymetsző pontjai határozzák meg a téglalap csúcspontjait. Ebből a tényből, valamint abból, hogy a három egymást metsző négyzet egy oktaédert határoz meg, egyértelműen következik, hogy az oktaéder éleinek aranymetsző pontjai egy ikozaéder csúcspontjainak felelnek meg.
Aranyszögnek nevezik azt a szöget, melynek koszinusza az aranymetszés hányadosa: cosALFA=0,618034... Ennek értéke: ALFA=51 fok, 49 perc, 43 másodperc. Az aranyszög számos díszítő alakzaton felfedezhető. A középkor építészei, művészei az arány isteni eredetének megfelelően az aranymetszésnek és az aranyszögnek különös jelentőséget tulajdonítottak. Azok a szimbólumok, jelképek, melyek az Ég és a Föld viszonyára vonatkoznak, az aranymetszési arány hordozói.
A
z aranyszöggel számos misztikus jelképet hordozó relikvián találkozni lehet. Aranyszöget zárnak be a Krisztus-monogram X jelének szárai a P betű szárával, és aranyszöget fedezhetünk fel Szent István királyunk REX ST (Rex Stephanus) betűjeleket tartalmazó ligatúrás kézjegyén is.
Pizza városában a XII. és XIII. század fordulóján élt egy Leonardo Pisano nevű matematikus, akit ma inkább Fibonacci néven ismerünk. A Liber Abaci című munkájában található a következő probléma, amit Fibonacci nyulaiként is szoktak emlegetni: "Hány pár nyúlra szaporodik egy év alatt a kezdeti pár, ha tudjuk, hogy a nyulak két hónap alatt válnak ivaréretté, és ezután minden pár minden hónapban egy új párnak ad életet és mindegyikük életben marad?" Az egyes hónapokhoz tartozó nyúl párok számát leíró: 1, 1, 2, 3, 5, 8, 13, 21, 34... számsor Fibonacci-sorozat néven vonult be a matematika történetébe.
A sorozat előállításának alapja az a tulajdonság, mely szerint a harmadik elemtől kezdve bármely elem az előző kettő összege. A sorozat első két elemét azonban meg kell adni. Ezek értéke a Fibonacci-sorozat esetén 1. A sorozat bármely két elemének hányadosa folyamatosan közelít az aranymetszés értékéhez, pontosabban akörül ugrál. A közelítés kétoldali, mert a két egymást követő elem hányadosa nagyobb, illetve kisebb, mint a közrefogott aranyszám. Ennek alapján azokat a négyzeteket, amelyek oldalainak mérőszámai a Fibonacci-sorozat elemei, Fibonacci-négyzeteknek nevezik.
Roger Penrose oxfordi matematikus 1973-ban fedezte fel a sík nem periodikus parkettázásának lehetőségét. Martin Gardner révén vált ismertté a felfedezése, mely 1977 januárjában jelent meg a Scientific American-ben Matematikai játékok címen. Az 1980-as évek elején újra fontos témává vált, a három dimenzióra történő általánosításának következtében.
A Penrose-csempék alakja különféle lehet, de a legérdekesebb és legismertebb pár a dárdák (konkáv rész) és sárkányok (konvex rész) kettőse. A csempék aranyrombuszokból készíthetőek, melyek szögeiknek nagysága 72° és 108°. Ha felosztjuk a rombusz hosszabbik átlóját az aranymetszés szerint, és az aranymetsző-pontot összekötjük a tompaszögű csúcsokkal, majd e két szakasz mentén kettévágjuk a rombuszt, egy konvex és egy konkáv, de egymással páronként megegyező oldalhosszúságú deltoidot kapunk. Oldalhosszainak aránya éppen fi.
Egy Ammann nevű matematikus Penrose ötletét tovább fejlesztve sokmindent fölfedezett még a témában, például az arany romboédereket. Az 1980-as évek elején számos természettudós és matematikus kezdte fontolóra venni annak lehetőségét, hogy a kristályok atomi szerkezete esetleg alapulhat egy nem periodikus hálózaton is (kvázi kristályok). Ezt követően 1984-ben Dany Schechtman és kollégái bejelentették, hogy nem periodikus szerkezetet találtak egy hirtelen lehűtött alumínium-mangán ötvözetnek az elektronmikroszkópos vizsgálata során. Ezt Schechtmanitnak nevezték el. A mikroszkópban látható ötszöges szimmetria egy, a Penrose-csempézéssel analóg, nem periodikus csempemintának felel meg a térben.
2. AMI NEM KÖZISMERT
Ha egy hosszú papírszalagon 5x180 fokot csavarunk balra vagy jobbra, majd a két végét összeragasztjuk, és a kapott szalagot középen kilyukasztva, hosszában körbevágjuk, akkor egy nagy gubancot kapunk. Ezt kifeszítve észrevehetjük, hogy egy 12x180 fokot csavarodó hurkot kaptunk, amit egy pentagramma formájába lehet szabályosan elrendezni. A szalag topológiai szempontból ekvivalens a téridő forrásának, más nevein a Mindenhatónak, Istenfiúnak, Brahmának a hullámterét leíró időtopológiai modellekkel.
A térszerán keletkezésekor egy időforrásból öt plusz egy darab (másolat) lesz az időhurokban. Ezek mindegyike olyan gömbszerű hullámteret áraszt magából, ami topológiailag kétoldalú és a belőle vágott szalag 360 fokos csavarodást tartalmaz. Így 12x180 = 6x360.
A jobbos csavarodású szalag a téridő forrásrendszerét modellezi, a balos az antitéridőét. A kétféle hullámtér kölcsönhatásba kerülve annihilálja egymás forrásrendszerét. Kölcsönösen megsemmisítik egymást. Ennek fizikai okai vannak, vagyis semmi köze holmi jó és rossz közötti harchoz, ahogy azt a misztikusok magyarázták régebben, nem ismervén a teremtés fizikáját. A pentagramma, mint az Isten (öt Atya) szimbóluma tehát kétféle lehet. A Mindenható a mi univerzumunk keltője, míg az Antimindenható az antiuniverzumot kelti. A pentagramma rezonátorként működik, mert formailag ezen felsőbb létezők önrezgését idézi meg. Ez okból használták régen varázsláshoz, az isteni erő megidézésére.
Ha megszerkesztjük körzővel és vonalzóval a tachion visszakanyarodását a saját múltjába, és megnézzük, hogy az egyes forráslátomások a körvonalon hol helyezkednek el (a kör közepéből nézve), akkor azt látjuk, hogy a pontok által bezárt szögek aránya elölről hátrafelé haladva (a jelentől a múlt felé) nagyjából ilyen: 1, 1, 2, 3, 5. Mert senki sem tökéletes, hanem csak az Atya. Eme szabályosság miatt hívják az univerzum központi térforrását (az Istent) tökéletesnek, mert a működésének, önkeltési arányainak alapja az aranymetszés.
Ennek megfelelően a Napisten, a Naprendszer lokális megtartója, aki a főbrahma helyi másolata, az Aranyvárosban lakik. Ez egy óriási, dimenzióbuborékkal védett város, ami a Nap belsejében lebeg és térugrásokkal áthelyeződve változtatja helyét a csillagban. Rendkívül szigorúan védik az angyalok (mennyei sereg), ezért ide bejutni csak a Napisten engedélyével lehet (a kellő szinten beavatott lelkek számára).
Készült: 2006.11.24.
esemenyhorizont magazin

 „Ahogy a számok szentek voltak a püthagoreusok számára, ugyanígy az ókori görögök a geometriát tekintették szakrális tudománynak- ez volt ugyanis az érvelés legmegfoghatóbb és ugyanakkor legelvontabb formája.”
„Ahogy a számok szentek voltak a püthagoreusok számára, ugyanígy az ókori görögök a geometriát tekintették szakrális tudománynak- ez volt ugyanis az érvelés legmegfoghatóbb és ugyanakkor legelvontabb formája.” A felsorolt síkidomok, magukban is tiszta formák.
A felsorolt síkidomok, magukban is tiszta formák.


 A Nagy Piramis geometriája
A Nagy Piramis geometriája







 Leonardo megmérte az ember csontszerkezetének pontos arányait. Õ volt az elsõ, aki kimutatta, hogy az emberi test a szó szoros értelmében építõkövekbõl áll, amelyek arányszáma mindig a phi-vel egyenlõ. Mi valójában valamennyien két lábon járó emlékmûvei vagyunk az aranymetszésnek.
Leonardo megmérte az ember csontszerkezetének pontos arányait. Õ volt az elsõ, aki kimutatta, hogy az emberi test a szó szoros értelmében építõkövekbõl áll, amelyek arányszáma mindig a phi-vel egyenlõ. Mi valójában valamennyien két lábon járó emlékmûvei vagyunk az aranymetszésnek.









 Adjunk egy kis szabadságot az elménknek! A harmónia a dolgok, események, érzelmek egymáshoz fűződő viszonya, amit mindig egy esztétikai értékrend és a mögötte álló filozófia határoz meg. Létezik-e az abszolút harmónia? Mert ha igen, akkor a korreláció fordított, s nem az értékrend és filozófia határozza meg az abszolút harmóniát, hanem inkább emez definiálja amazokat. Márpedig az abszolút fogalmak kifejezhetők, vagy mondjuk úgy, tömöríthetők az algebra nyelvén.
Adjunk egy kis szabadságot az elménknek! A harmónia a dolgok, események, érzelmek egymáshoz fűződő viszonya, amit mindig egy esztétikai értékrend és a mögötte álló filozófia határoz meg. Létezik-e az abszolút harmónia? Mert ha igen, akkor a korreláció fordított, s nem az értékrend és filozófia határozza meg az abszolút harmóniát, hanem inkább emez definiálja amazokat. Márpedig az abszolút fogalmak kifejezhetők, vagy mondjuk úgy, tömöríthetők az algebra nyelvén. Mindig is vonzott a tánc művészete, leginkább az indiai klasszikus táncok ragadtak meg. A nyugati festőművészetben talán Degas táncosnő-képei a legismertebbek. Ezek a balerinák szinte súlytalanok, tökéletes arányokkal mozdulnak, a képeken a tánc éteri minősége tölti fel testüket és ruházatukat. Szerettem volna tetten érni a légiesség eme technikai lényegét. Magam is próbálkoztam a táncoló női alak ábrázolásával, kucsipudi, manipuri és kathaki táncosnőket rajzoltam meg. Az első pillanatban azt gondolná az ember, egy-két könnyed vonal, és kész is az alkotás. A valóság azonban kicsit eltér ettől. A tánc – és főként az indiai klasszikus tánc – mozdulatai mértani pontosságúak, valószínűleg nem tudatosan, inkább rutinszerűen. A kép csak akkor sikerülhet, ha megtaláljuk az arányokat, és szinte megszerkesztjük a képet mozdulataiban.
Mindig is vonzott a tánc művészete, leginkább az indiai klasszikus táncok ragadtak meg. A nyugati festőművészetben talán Degas táncosnő-képei a legismertebbek. Ezek a balerinák szinte súlytalanok, tökéletes arányokkal mozdulnak, a képeken a tánc éteri minősége tölti fel testüket és ruházatukat. Szerettem volna tetten érni a légiesség eme technikai lényegét. Magam is próbálkoztam a táncoló női alak ábrázolásával, kucsipudi, manipuri és kathaki táncosnőket rajzoltam meg. Az első pillanatban azt gondolná az ember, egy-két könnyed vonal, és kész is az alkotás. A valóság azonban kicsit eltér ettől. A tánc – és főként az indiai klasszikus tánc – mozdulatai mértani pontosságúak, valószínűleg nem tudatosan, inkább rutinszerűen. A kép csak akkor sikerülhet, ha megtaláljuk az arányokat, és szinte megszerkesztjük a képet mozdulataiban.